Bloom Filter
Problem statement
In their current format, column statistics and dictionaries can be used for predicate pushdown. Statistics include minimum and maximum value, which can be used to filter out values not in the range. Dictionaries are more specific, and readers can filter out values that are between min and max but not in the dictionary. However, when there are too many distinct values, writers sometimes choose not to add dictionaries because of the extra space they occupy. This leaves columns with large cardinalities and widely separated min and max without support for predicate pushdown.
A Bloom filter is a compact data structure that overapproximates a set. It can respond to membership queries with either “definitely no” or “probably yes”, where the probability of false positives is configured when the filter is initialized. Bloom filters do not have false negatives.
Because Bloom filters are small compared to dictionaries, they can be used for predicate pushdown even in columns with high cardinality and when space is at a premium.
Goal
Enable predicate pushdown for high-cardinality columns while using less space than dictionaries.
Induce no additional I/O overhead when executing queries on columns without Bloom filters attached or when executing non-selective queries.
Technical Approach
The section describes split block Bloom filters, which is the first (and, at time of writing, only) Bloom filter representation supported in Parquet.
First we will describe a “block”. This is the main component split block Bloom filters are composed of.
Each block is 256 bits, broken up into eight contiguous “words”, each consisting of 32 bits. Each word is thought of as an array of bits; each bit is either “set” or “not set”.
When initialized, a block is “empty”, which means each of the eight
component words has no bits set. In addition to initialization, a
block supports two other operations: block_insert and
block_check. Both take a single unsigned 32-bit integer as input;
block_insert returns no value, but modifies the block, while
block_check returns a boolean. The semantics of block_check are
that it must return true if block_insert was previously called on
the block with the same argument, and otherwise it returns false
with high probability. For more details of the probability, see below.
The operations block_insert and block_check depend on some
auxiliary artifacts. First, there is a sequence of eight odd unsigned
32-bit integer constants called the salt. Second, there is a method
called mask that takes as its argument a single unsigned 32-bit
integer and returns a block in which each word has exactly one bit
set.
unsigned int32 salt[8] = {0x47b6137bU, 0x44974d91U, 0x8824ad5bU,
0xa2b7289dU, 0x705495c7U, 0x2df1424bU,
0x9efc4947U, 0x5c6bfb31U}
block mask(unsigned int32 x) {
block result
for i in [0..7] {
unsigned int32 y = x * salt[i]
result.getWord(i).setBit(y >> 27)
}
return result
}
Since there are eight words in the block and eight integers in the
salt, there is a correspondence between them. To set a bit in the nth
word of the block, mask first multiplies its argument by the nth
integer in the salt, keeping only the least significant 32 bits of
the 64-bit product, then divides that 32-bit unsigned integer by 2 to
the 27th power, denoted above using the C language’s right shift
operator “>>”. The resulting integer is between 0 and 31,
inclusive. That integer is the bit that gets set in the word in the
block.
From the mask operation, block_insert is defined as setting every
bit in the block that was also set in the result from mask. Similarly,
block_check returns true when every bit that is set in the result
of mask is also set in the block.
void block_insert(block b, unsigned int32 x) {
block masked = mask(x)
for i in [0..7] {
for j in [0..31] {
if (masked.getWord(i).isSet(j)) {
b.getWord(i).setBit(j)
}
}
}
}
boolean block_check(block b, unsigned int32 x) {
block masked = mask(x)
for i in [0..7] {
for j in [0..31] {
if (masked.getWord(i).isSet(j)) {
if (not b.getWord(i).setBit(j)) {
return false
}
}
}
}
return true
}
The reader will note that a block, as defined here, is actually a special kind of Bloom filter. Specifically it is a “split” Bloom filter, as described in section 2.1 of Network Applications of Bloom Filters: A Survey. The use of multiplication by an odd constant and then shifting right is a method of hashing integers as described in section 2.2 of Dietzfelbinger et al.’s A reliable randomized algorithm for the closest-pair problem.
This closes the definition of a block and the operations on it.
Now that a block is defined, we can describe Parquet’s split block
Bloom filters. A split block Bloom filter (henceforth “SBBF”) is
composed of z blocks, where z is greater than or equal to one and
less than 2 to the 31st power. When an SBBF is initialized, each block
in it is initialized, which means each bit in each word in each block
in the SBBF is unset.
In addition to initialization, an SBBF supports an operation called
filter_insert and one called filter_check. Each takes as an
argument a 64-bit unsigned integer; filter_check returns a boolean
and filter_insert does not return a value, but does modify the SBBF.
The filter_insert operation first uses the most significant 32 bits
of its argument to select a block to operate on. Call the argument
“h”, and recall the use of “z” to mean the number of blocks. Then
a block number i between 0 and z-1 (inclusive) to operate on is
chosen as follows:
unsigned int64 h_top_bits = h >> 32;
unsigned int64 z_as_64_bit = z;
unsigned int32 i = (h_top_bits * z_as_64_bit) >> 32;
The first line extracts the most significant 32 bits from h and
assigns them to a 64-bit unsigned integer. The second line is
simpler: it just sets an unsigned 64-bit value to the same value as
the 32-bit unsigned value z. The purpose of having both h_top_bits
and z_as_64_bit be 64-bit values is so that their product is a
64-bit value. That product is taken in the third line, and then the
most significant 32 bits are extracted into the value i, which is
the index of the block that will be operated on.
After this process to select i, filter_insert uses the least
significant 32 bits of h as the argument to block_insert called on
block i.
The technique for converting the most significant 32 bits to an
integer between 0 and z-1 (inclusive) avoids using the modulo
operation, which is often very slow. This trick can be found in
Kenneth A. Ross’s 2006 IBM research report, “Efficient Hash Probes on
Modern Processors”
The filter_check operation uses the same method as filter_insert
to select a block to operate on, then uses the least significant 32
bits of its argument as an argument to block_check called on that
block, returning the result.
In the pseudocode below, the modulus operator is represented with the C
language’s “%” operator. The “>>” operator is used to denote the
conversion of an unsigned 64-bit integer to an unsigned 32-bit integer
containing only the most significant 32 bits, and C’s cast operator
“(unsigned int32)” is used to denote the conversion of an unsigned
64-bit integer to an unsigned 32-bit integer containing only the least
significant 32 bits.
void filter_insert(SBBF filter, unsigned int64 x) {
unsigned int64 i = ((x >> 32) * filter.numberOfBlocks()) >> 32;
block b = filter.getBlock(i);
block_insert(b, (unsigned int32)x)
}
boolean filter_check(SBBF filter, unsigned int64 x) {
unsigned int64 i = ((x >> 32) * filter.numberOfBlocks()) >> 32;
block b = filter.getBlock(i);
return block_check(b, (unsigned int32)x)
}
The use of blocks is from Putze et al.’s Cache-, Hash- and Space-Efficient Bloom filters
To use an SBBF for values of arbitrary Parquet types, we apply a hash function to that value - at the time of writing, xxHash, using the function XXH64 with a seed of 0 and following the specification version 0.1.1.
Sizing an SBBF
The check operation in SBBFs can return true for an argument that
was never inserted into the SBBF. These are called “false
positives”. The “false positive probability” is the probability that
any given hash value that was never inserted into the SBBF will
cause check to return true (a false positive). There is not a
simple closed-form calculation of this probability, but here is an
example:
A filter that uses 1024 blocks and has had 26,214 hash values
inserted will have a false positive probability of around 1.26%. Each
of those 1024 blocks occupies 256 bits of space, so the total space
usage is 262,144. That means that the ratio of bits of space to hash
values is 10-to-1. Adding more hash values increases the denominator
and lowers the ratio, which increases the false positive
probability. For instance, inserting twice as many hash values
(52,428) decreases the ratio of bits of space per hash value inserted
to 5-to-1 and increases the false positive probability to
18%. Inserting half as many hash values (13,107) increases the ratio
of bits of space per hash value inserted to 20-to-1 and decreases the
false positive probability to 0.04%.
Here are some sample values of the ratios needed to achieve certain false positive rates:
Bits of space per insert | False positive probability |
|---|---|
| 6.0 | 10 % |
| 10.5 | 1 % |
| 16.9 | 0.1 % |
| 26.4 | 0.01 % |
| 41 | 0.001 % |
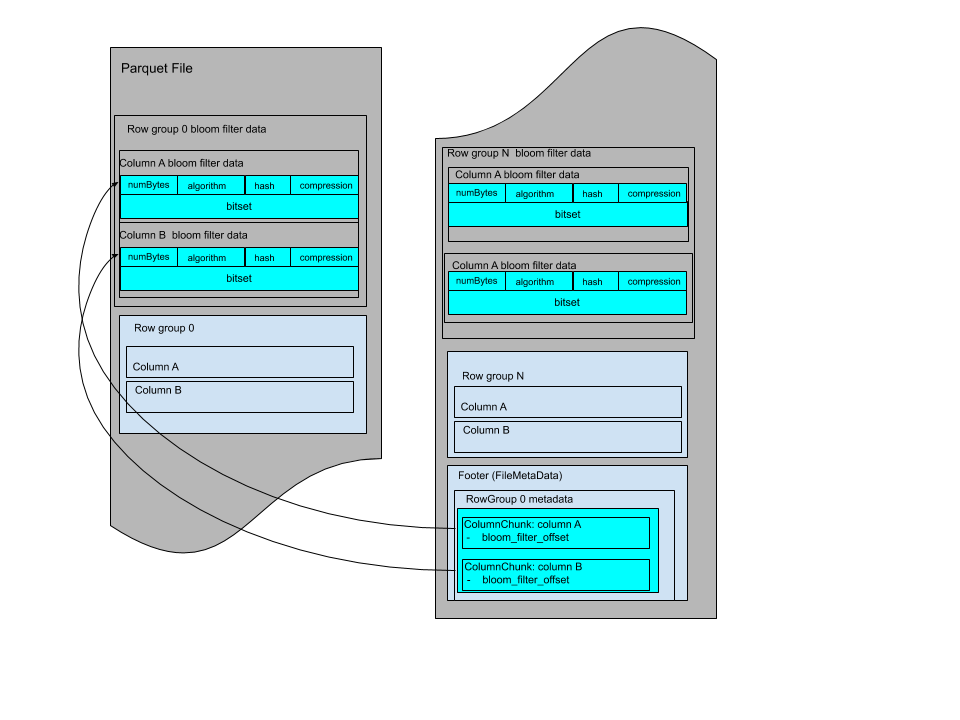
File Format
Each multi-block Bloom filter is required to work for only one column chunk. The data of a multi-block bloom filter consists of the bloom filter header followed by the bloom filter bitset. The bloom filter header encodes the size of the bloom filter bit set in bytes that is used to read the bitset.
Here are the Bloom filter definitions in thrift:
/** Block-based algorithm type annotation. **/
struct SplitBlockAlgorithm {}
/** The algorithm used in Bloom filter. **/
union BloomFilterAlgorithm {
/** Block-based Bloom filter. **/
1: SplitBlockAlgorithm BLOCK;
}
/** Hash strategy type annotation. xxHash is an extremely fast non-cryptographic hash
* algorithm. It uses 64 bits version of xxHash.
**/
struct XxHash {}
/**
* The hash function used in Bloom filter. This function takes the hash of a column value
* using plain encoding.
**/
union BloomFilterHash {
/** xxHash Strategy. **/
1: XxHash XXHASH;
}
/**
* The compression used in the Bloom filter.
**/
struct Uncompressed {}
union BloomFilterCompression {
1: Uncompressed UNCOMPRESSED;
}
/**
* Bloom filter header is stored at beginning of Bloom filter data of each column
* and followed by its bitset.
**/
struct BloomFilterPageHeader {
/** The size of bitset in bytes **/
1: required i32 numBytes;
/** The algorithm for setting bits. **/
2: required BloomFilterAlgorithm algorithm;
/** The hash function used for Bloom filter. **/
3: required BloomFilterHash hash;
/** The compression used in the Bloom filter **/
4: required BloomFilterCompression compression;
}
struct ColumnMetaData {
...
/** Byte offset from beginning of file to Bloom filter data. **/
14: optional i64 bloom_filter_offset;
}
The Bloom filters are grouped by row group and with data for each column in the same order as the file schema.
The Bloom filter data can be stored before the page indexes after all row groups. The file layout looks like:

Or it can be stored between row groups, the file layout looks like:
Encryption
In the case of columns with sensitive data, the Bloom filter exposes a subset of sensitive information such as the presence of value. Therefore the Bloom filter of columns with sensitive data should be encrypted with the column key, and the Bloom filter of other (not sensitive) columns do not need to be encrypted.
Bloom filters have two serializable modules - the PageHeader thrift structure (with its internal
fields, including the BloomFilterPageHeader bloom_filter_page_header), and the Bitset. The header
structure is serialized by Thrift, and written to file output stream; it is followed by the
serialized Bitset.
For Bloom filters in sensitive columns, each of the two modules will be encrypted after serialization, and then written to the file. The encryption will be performed using the AES GCM cipher, with the same column key, but with different AAD module types - “BloomFilter Header” (8) and “BloomFilter Bitset” (9). The length of the encrypted buffer is written before the buffer, as described in the Parquet encryption specification.